

When two waves of slightly different frequency overlap a phenomenon
known as beats results. The effect is a kind of throbbing sensation, which can sometimes be
heard when two musicians such as oboeists are playing together.
If they are
attempting to play the same note but are fractionally out of tune with each other beats will be
heard: the frequency will vary about a mean value. The closer the two frequencies the lower
will be the beat frequency, and this will become zero when they are perfectly in tune. The
human ear is normally very sensitive to pitch and the two notes have to be well within one
semitone for true beats to be heard.
Even if we take C and B on the musicians'
scale, one semitone apart, the beat frequency would be 261.6 - 247 = 14.6 Hz, that is, nearly
fifteen beats per second! This would not give audible beats, only an unpleasant
discord.
Consider two waves of slightly different frequencies f1 and f2 (f1 > f2) but of
the same amplitude. Figure 1 is a diagram of the two waves and their resultant.
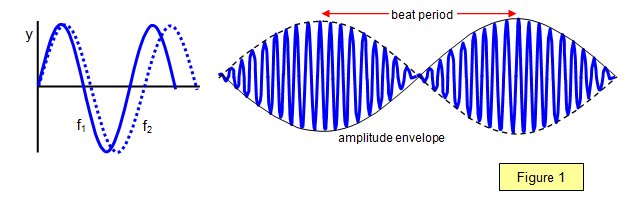
The addition of two or more waves at a point to give a resultant
disturbance uses the principle of superposition. This states that the final disturbance is simply
the vector sum of each disturbance at that point. The principle is used in the equations for
standing waves, beats, diffraction and interference.
The effect can easily be observed in
the laboratory with two signal generators and loudspeakers.
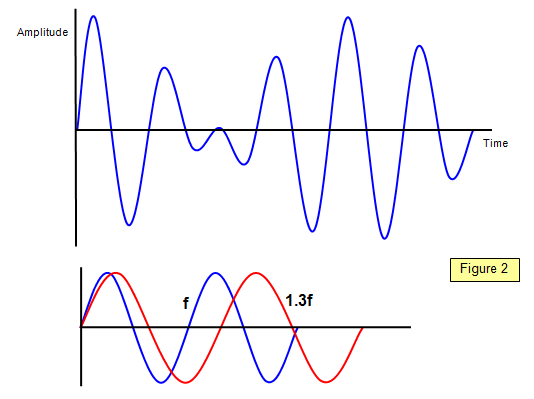
The diagrams in Figure 2 show the result of
adding two waves, one of frequency f and the other of frequency 1.3f.
Beats are
used in police radar speed traps. The outgoing and reflected signals are fed to the detector
and the speed of the car is determined from the beat frequency using the Doppler shift.

